FV, czyli wartość przyszła pojedynczego przepływu pieniężnego – kapitalizacja podokresowa
Bardzo często spotykanym zjawiskiem w praktyce jest występowanie tzw. kapitalizacji podokresowej. Mianowicie, rzadko zdarza się, że bank wypłaca swoim klientom odsetki od depozytów wyłączenie raz na rok. W rzeczywistości płatność występuje przynajmniej raz w miesiącu, lub częściej (np. codziennie). W takich przypadkach, nie jest możliwe, aby poprawnie obliczyć końcową wielkość powierzonego kapitału przy wykorzystaniu podstawowego wzoru na przyszłą wartość pojedynczego przepływu pieniężnego. Dlatego też, w tym artykule, wyjaśnię w jaki sposób zastosować formułę uwzględniającą kapitalizację podokresową.
Należy zaznaczyć, że przedmiotem artykułu jest wartość przyszła pojedynczego przepływu pieniężnego. To znaczy, że analizowane sytuację dotyczą np. jednorazowej wpłaty na konto/lokatę. Dodatkowo, zakłada się, że przez cały czas trwania tej inwestycji nie dokonuje się żadnych innych wypłat, ani wpłat. Istotne jest, że w przypadku omawianej teorii występuje zjawisko kapitalizacji odsetek. To oznacza, że są one wypłacane na to samo konto, na którym znajduje się depozyt, czyli każda wypłata powiększy wartość zainwestowanego kapitału. Dodatkowo, w każdym kolejnym okresie wysokość odsetek będzie wyższa, ponieważ wartość kapitału stopniowo rośnie z okresu na okres. Tą zależność dokładniej przedstawiłem w artykule, w którym wyjaśniłem istotę oprocentowania składanego.
Wzór na wartość przyszłą przy kapitalizacji podokresowej
Zastosowanie kapitalizacji podokresowej związane jest z wykorzystaniem odpowiedniej formuły, która pozwala na ustalenie wartości kapitału końcowego. Jest ona pewnego rodzaju rozwinięciem podstawowej wersji wzoru, który uwzględnia oprocentowanie składane. Formuła ma następującą postać[1]:

Należy wyjaśnić, że jest to najczęściej spotykany w literaturze wariant wzoru na wartość przyszłą kapitału początkowego. Niemniej jednak, taka forma prezentacji omawianego równania nie jest w pełni poprawna. Zgodnie z zasadami algebry Iloczyn przedstawiany jest poprzez postawienie dwóch wyrazów wzoru obok siebie (bez znaku pomiędzy nimi). W ten sposób zaprezentowane jest wyrażenie „tn”, czyli iloczyn liczby lat i kapitalizacji w ciągu jednego roku. Natomiast we wzorze dodatkowo wykorzystano np. wyraz „PV”, który nie jest iloczynem dwóch elementów „P” i „V”. Dlatego też, bardziej poprawnym rozwiązaniem wydaje się być wykorzystywanie liter „F” i „P”, tak jak w podręczniku M. Podgórskiej i J. Klimkowskiej[2].
Ważne jest, aby pamiętać, że w różnych podręcznikach w odmienny sposób nazwane zostaną poszczególne elementy wzoru. Na przykład, bardzo często zamiast litery „i” wykorzystuje się literę „r”, często dodawane są również indeksy dolne.
Kapitalizacja podokresowa – podstawowe pojęcia
Do zastosowania metodyki, która uwzględnia kapitalizację podokresową wymagana jest znajomość kilku pojęć związanych z teorią wartości pieniądza w czasie. Te terminy zostały wyjaśnione w artykule, który został w całości poświęcony oprocentowaniu składanemu. Niemniej jednak, należy zwięźle wyjaśnić, że:
- Wartość obecna (PV; present value) – na przykład są to środki, które powierzono bankowi w chwili otwarcia lokaty.
- Wartość przyszła (FV; future value) – kapitał powiększony o narosłe odsetki. W uproszczeniu jest to kwota, którą otrzymamy w rezultacie otwarcia lokaty, po jej (terminowym) zakończeniu.
- Oprocentowanie roczne (i; nominal annual interest rate) – odnosi się ono do rocznego nominalnego oprocentowania np. depozytu.
- Liczba kapitalizacji w roku (n; numer of compounding periods per year) – jest to liczba wypłat odsetek w ciągu roku. To znaczy, że w przypadku, gdy odsetki wypłacane są raz na miesiąc to „n” będzie równe 12, gdy co kwartał to n wyniesie 4 itd.
- Liczba lat (t) – czas wyrażony w latach.
Oprócz podstawowych pojęć, bardzo przydatne jest wprowadzenie dwóch dodatkowych terminów. Są one bezpośrednio powiązane z opisanymi pojęciami. Niemniej jednak, w dużym stopniu ułatwiają zastosowanie funkcji finansowych arkusza kalkulacyjnego (np. MS Excel). Są to:
- RATE – to iloraz rocznego oprocentowania i liczby kapitalizacji występujących w jednym roku ( i/n ). W przypadku depozytu oprocentowanego 6% w skali roku i uwzględniającego co miesięczną wypłatę odsetek, parametr RATE wyniesie 0,5% (6%/12).
- NPER – jest to iloczyn czasu wyrażonego w latach oraz liczby kapitalizacji występujących w ciągu jednego roku ( t x n ). Inaczej jest to liczba wszystkich okresów. Na przykład, gdy otwieramy 3-letnią lokatę, która wypłaca odsetki raz na miesiąc to łączna liczba okresów wyniesie 36 (3 x 12).
Wartość przyszła (FV) przy kapitalizacji podokresowej – przykłady
Ustalenie przyszłej wartości kapitału przy zastosowanie kapitalizacji podokresowej wymaga zastosowania przedstawionego wcześniej wzoru. Dodatkowo, wykorzystanie omawianej metody uwidacznia bardzo interesującą zależność występującą pomiędzy wartością przyszłą i liczbą kapitalizacji w jednym roku. W celu ukazania tej relacji należy przeanalizować następujące przykłady:
- W banku założony został depozyt w wysokości 1000 zł. Oprocentowanie wynosi 5% w skali roku, a odsetki wypłacane są raz na pół roku (2 razy w roku; n=2). Jaka będzie wartość tego depozytu po okresie 2 lat?

- Rozważmy podobny przykład, niemniej jednak, w tym przypadku odsetki wypłacane są raz na kwartał (4 razy w roku; n=4):
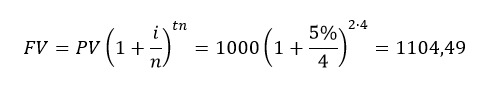
- Przykłady ukazały następująca zależność – wartość przyszła depozytu będzie tym wyższa im częściej wypłacane są odsetki w ciągu roku. Łatwo to sprawdzić analizując dwa, kolejne depozyty. W ich przypadku odsetki wypłacane są raz na miesiąc (12 razy w roku; n=12) i codziennie (365 razy w roku; n=365 przy założeniu, że rok ma 365 dni):
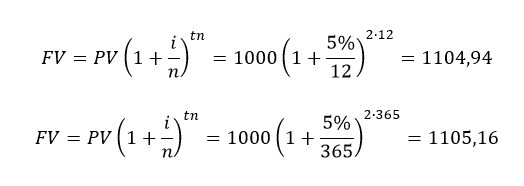
Podsumowując, można stwierdzić, iż im większa jest liczba kapitalizacji w ciągu roku tym wyższa będzie wartość przyszła. Istotne jest, że nominalne oprocentowanie jest identyczne w każdym przypadku, natomiast inwestor efektywnie zarabia tym więcej im częściej wypłacane są odsetki. W takiej sytuacji możliwe jest obliczenie tzw. efektywnej stopy procentowej, która odzwierciedla rzeczywisty zysk właściciela depozytu. Ta metoda zostanie przeze mnie opisane w odrębnym artykule.
Warto dodać, iż istnieje możliwość obliczenia wartości kapitału końcowego przy ciągłej kapitalizacji. W takim przypadku korzysta się z innego wzoru, który jest wynikiem obliczenia granicy funkcji (gdzie „n” dąży do nieskończoności). Gdyby założyć, że w poprzednim przykładzie mamy do czynienia z kapitalizacją ciągłą to wartość przyszłą można obliczyć w następujący sposób:
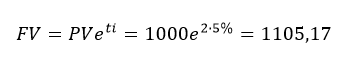
Wartość przyszła (FV) w MS Excel
Obliczenia związane z kapitalizacją podokresową jest bardzo łatwo przeprowadzić w arkuszu kalkulacyjnym. W tym przypadku wykorzystany zostanie MS Excel. Mianowicie, posiada on wbudowaną funkcję „FV”, która po wprowadzeniu argumentów zwraca odpowiedni wynik. Przypominam, że zostały one krótko scharakteryzowałem na początku artykułu. Do zastosowania kapitalizacji podokresowej niezbędne są następujące argumenty:
- RATE (stopa) – jest to procentowane przypadające na jeden okres,
- NPER (liczba_rat) – całkowita liczba okresów,
- [pv] ([wa]) – wartość bieżąca.
Należy wyjaśnić, że podałem dwie nazwy argumentów – w nawiasach występują te, które zostały opisane w składni funkcji „FV” w polskiej wersji arkusza kalkulacyjnego. Zaznaczam, że polskie nazwy są w dużym stopniu mylące, z uwagi na fakt, iż nazwy anglojęzyczne są jednocześnie nazwami funkcji, które służą do obliczenia poszczególnych elementów równania. Na przykład znając wartość przyszłą, obecną i oprocentowanie możemy obliczyć liczbę okresów wykorzystując funkcję NPER. Składnia funkcji FV jest następująca (pierwsza z wymienionych w języku angielskim, druga w polskim):
- FV(rate,nper,pmt,[pv],[type])
- FV(stopa;liczba_okresów;rata;[wb];[typ])
Podsumowując, istnieje np. funkcja NPER, która dotyczy ilości okresów i wykorzystuje się ją pod tą nazwą zarówno w arkuszu w języku polskim, jak i angielskim. Natomiast nie istnieje funkcja „liczba_okresów”, która jest drugim argument funkcji „FV” w polskiej wersji programu MS Excel. Zaznaczam, że ten problem dotyczy wersji 2016.
Wartość przyszła (FV) – przykłady w MS Excel (funkcja FV, RATE i NPER)
Wszystkie przykłady, które przedstawiono w niniejszym artykule zostały obliczone w arkuszu kalkulacyjnym. W tym celu wykorzystano funkcję „FV”, a także ręcznie wprowadzono formuły/wzory. Dodatkowo, do obliczeń wykorzystane zostały dwie funkcję programu Excel: NPER i RATE. W tej części artykułu przedstawione zostaną przykłady zastosowania funkcji arkusza kalkulacyjnego. W pierwszej kolejności, zaprezentowane będzie zastosowanie funkcji RATE i NPER, a następnie wszystkie wcześniej obliczone przykłady (z wyjątkiem kapitalizacji ciągłej) zostaną rozwiązane za pomocą funkcji FV.
Zastosowanie funkcji NPER i RATE
Tak jak wspomniano wcześniej, funkcja NPER pozwala na obliczenie liczby okresów, które są potrzebne, aby przy danym oprocentowaniu kapitał zwiększył swoją wartość do wartości przyszłej. Funkcja RATE pozwala na określenie oprocentowania, które pozwoli na zwiększenie wartości kapitału do określonej kwoty w danym czasie. To znaczy:
- Funkcja NPER odpowiada na pytanie: Ile czasu potrzebuję, aby mój depozyt zwiększył swoją wartość do danej kwoty przy określonym oprocentowaniu?
- Funkcja RATE odpowiada na pytanie: Jakie powinno być oprocentowanie depozytu, aby w danym czasie zwiększył on swoją wartość do określonej kwoty?
Należy jednak pamiętać, że powyższe pytania dotyczą wartości przyszłej pojedynczego przepływu pieniężnego. Mianowicie, żadne regularne wpłaty na konto nie są brane pod uwagę. Dlatego też, w przedstawionych przykładach pominięty zostanie argument PMT (po polsku „rata”). Rozważmy zatem dwie sytuacje dotyczące depozytów:
- Posiadamy depozyt o wartości 2000 zł, ale chcemy, aby jego wartość wzrosła do 4000 zł. Oprocentowanie roczne wynosi 7%, odsetki wypłacane są co miesiąc, więc miesięcznie jest ono równe (nominalnie) 7%/12=0,58%. Ile czasu (w miesiącach) będzie potrzebne, aby nasz kapitał zwiększył swoją wartość do 4000 zł?
- Depozyt o wartości 2000 zł nie zostanie wypłacony z banku dopóki jego wartość nie będzie równa 4000 zł. Jakie musiałoby być oprocentowanie tego depozytu, aby przy comiesięcznej wypłacie odsetek zwiększył on swoją wartość do poziomu 4000 zł w 2 lata (24 miesiące)?
Rozwiązanie tych problemów przedstawiono na rysunkach zamieszczonych poniżej. Należy zaznaczyć, że w składni funkcji wartość obecna (argument „wa”) została wprowadzona ze znakiem „minus”. Jest to krok obowiązkowy, który łatwo jest intuicyjnie wytłumaczyć. Mianowicie, musimy w pierwszej kolejności „wydać 2000 zł”, aby zarobić 4000zł w przyszłości.
Podsumowując stwierdza się, że do zwiększenia wartości depozytu z 2000 zł do 4000 zł potrzebne będzie ok. 119 miesięcy (czyli prawie 10 lat). Natomiast, aby ten cel osiągnąć w 2 lata to oprocentowanie (miesięczne) musiałoby wynosić ok. 2,93%.


Zastosowanie funkcji FV
W treści artykułu obliczone zostały przykłady dotyczące kapitalizacji podokresowej. Na rysunkach zamieszczonych poniżej przedstawione zostały formuły (i wyniki), które należało wprowadzić w odpowiednie komórki arkusza kalkulacyjnego, aby otrzymać identyczne rezultaty. Należy wyjaśnić, że:
- W wierszu 10 – znajdują się rezultaty wynikające z zastosowania wzoru na wartość przyszłą pojedynczego przepływu pieniężnego, który uwzględnia kapitalizacje podokresową.
- W wierszu 11 – znajdują się wyniki zastosowania funkcji „FV” dla poszczególnych przykładów. Zaznaczam, że:
- Argument „rata” (po angielsku „pmt”) został pominięty ponieważ przykłady dotyczą pojedynczych przepływów, a nie renty. To znaczy, że analizowane są przypadki jednorazowej wpłaty, bez cyklicznych dopłat, lub wypłat.
- Argument „[wa]” (po angielsku [pv] – present value) został wprowadzony ze znakiem minus. Jest to operacja, która pozwala na otrzymanie prawidłowego rezultatu.
- Argument „typ” został pominięty, ponieważ dotyczy serii przepływów pieniężnych oraz momentu, w którym one występują – na końcu, lub początku okresu. W przypadku omawianych przykładów występuje tylko pojedyncza płatność, dlatego też ten argument nie znajduje zastosowania.
- W wierszu 13 – dodatkowo zastosowano wcześniej omawianą funkcje NPER, która pozwala na obliczenie liczby okresów niezbędnych do zwiększenia pewnego kapitału początkowego do określonej wartości przyszłej przy danym oprocentowaniu. Te obliczenia zostały zaprezentowane wyłączenie w celach poglądowych, aby pokazać możliwości zastosowania tej funkcji.
- W wierszu 14 – znajdują się obliczenia z wykorzystaniem funkcji RATE – ukazano, że w przypadku znajomości wartości przyszłej, całkowitej liczby okresów i wartości obecnej możliwe jest obliczenie wysokości oprocentowania. Zastosowanie funkcji RATE przedstawione zostało w celach poglądowych.


Podsumowanie i plik MS Excel
Metodyka ustalania wartości przyszłej kapitału początkowego jest bardzo ważnym elementem teorii wartości pieniądza w czasie. Zastosowanie kapitalizacji podokresowej pozwala na rozwiązanie wielu problemów, które mają charakter praktyczny. Dla osób zainteresowanych zamieszczam plik programu Excel, w którym rozwiązane zostały opisane przykłady.
FV – wartość przyszła – kapitalizacja podokresowa
Źródła:
[1] Zob. R.A. Defusco, et. al., “Quantitative Investment Analysis”, Wiley, wyd. 2, 2007, s. 9.
[2] Zob. M. Podgórska, J. Klimkowska, „Matematyka Finansowa”, Wydawnictwo Naukowe PWN, Warszawa 2006, s. 78.



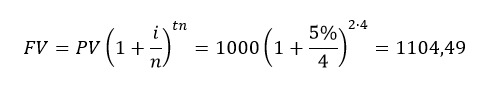
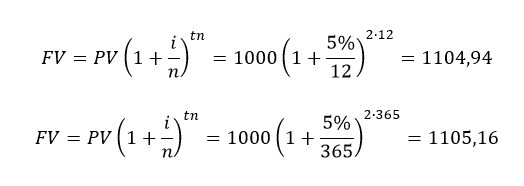
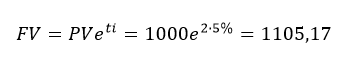





Trafiłam na Twojego bloga szukając informacji o FV przy okazji nauki różnych funkcji w Excelu (i próbie ich zrozumienia) i mam mocne postanowienie zaglądać tu częściej. Twój blog jest rewelacyjny – myślę, że założenie aby o rzeczach skomplikowanych mówić w przystępny sposób – “Jakie to łatwe!” udało Ci się w 100%. Naprawdę kawał świetnej roboty.
Witam,
Bardzo dziękuję za komentarz. Cieszę się, że mój blog się Pani przydał. Pozdrawiam serdecznie!
No niestety, lecz stosując Twoje rozwiązania, w excelu wychodzi mi zupełnie co innego…..
Cześć, napisz proszę, który przykład/zadanie masz na myśli, to postaram się pomóc.
Super wytłumaczone. Mam jednak problem. W pracy jeden współpracownik licząc obecną wartość rat liczy jako suma z FV/((1+i)^t/12), gdzie: “FV” wysokość miesięcznej raty (stała wartość), “i” to roczna stopa procentowa, “t” liczba miesięcy (od 1 do 24). Nie rozumiem dlaczego nie dzieli “i” przez 12 a ma w potędze to dzielenie. W funkcji w excelu wygląda to tak: PV((1+i)^(1/12)-1; 24; FV).
Cześć,
Wydaje mi się, że twój współpracownik postępuje właściwie, ale bardzo ważny jest tutaj kontekst w jakim przeprowadzane są obliczenia. Myślę, że o przyjętej metodyce decyduje odgórna procedura, lub np. przepisy umowne. Niemniej jednak, mogę jedynie „gdybać” ponieważ nie znam dokładnie zagadnienia. Uważam, że warto jest przeanalizować metodykę.
Zwróć uwagę, że wykorzystywana jest funkcja „PV”. Działa ona trochę inaczej niż wzór. Mianowicie, przyjmuje m.in.2 parametry – NPER i RATE. Pierwszy z wymienionych to całkowita liczba okresów (jest to 2-gi element składni funkcji). W tym przypadku, Twój kolega/koleżanka z pracy wprowadza 24, która odzwierciedla liczbę wszystkich miesięcy, dla 2-letniego okresu. Natomiast, parametr RATE jest stopą przypadającą na pojedynczy okres – czyli na jeden miesiąc.
Ważna rzeczą jest, że Twój współpracownik, do wzoru podstawia efektywną okresową stopę procentową – dokonuje konwersji rocznej stopy procentowej. W rezultacie, dowiaduje się, jaką stopę procentową musi podstawić, aby przy kapitalizacji przez 24 miesiące, obliczenia dały taki sam rezultat jakby podstawić wartość rocznej stopy procentowej i kapitalizować ją przez 2 lata. To znaczy, że formuła (podstawiam przykładowo 10% za „i” oraz 10000 za FV) – „PV((1+10%)^(1/12)-1; 24;;10000)” da taki sam rezultat co „PV(10%; 2;;10000)”, czyli -8 264,46 zł. Dzieje się tak ponieważ (zaokrąglam do 4 miejsc po przecinku):
Wobec tego nie wiadomo czy twój współpracownik postępuje prawidłowo, czy też nie. Wiadomo jednak co dokładnie robi, w kontekście przyjętej metodyki. Być może pewne zapisy powodują, że dana wartość ma być kapitalizowana w stosunku rocznym, ale określone kwoty wylicza się w ujęciu miesięcznym i stąd wystąpiła konieczność dokonania wspomnianego przekształcenia.
Mam nadzieję, że trochę pomogłem.
Pozdrawiam serdecznie
Dziękuję bardzo za wyjaśnienie! Bardzo pomogłeś 🙂