Istota CAGR
CAGR to średnia roczna stopa wzrostu, lub inaczej skumulowany roczny wskaźnik wzrostu (ang. Compound Annual Growth Rate). Jest to miara, która odzwierciedla średni roczny przyrost określonej wartości, na przestrzeni danego okresu. Należy podkreślić, że polskojęzyczna nazwa tej metody, którą przetłumaczono z języka angielskiego, jest bardzo nietrafiona. Nie odzwierciedla ona istoty CAGR, która wynika z zastosowania teorii wartości pieniądza w czasie, a dokładniej, zasady procentu złożonego (ang. compounded interest).
Istotę średniej rocznej stopy wzrostu można wyjaśnić na nieskomplikowanym przykładzie. W dużym uproszczeniu, można stwierdzić, że za pomocą CAGR, każdą inwestycje można przyrównać do lokaty bankowej, która wypłaca odsetki raz na rok. Mianowicie, do określenia wysokości średniej rocznej stopy wzrostu niezbędna jest informacja o wielkości kapitału początkowego, o jego wartości końcowej, a także o czasie trwania inwestycji. Na przykład, wartość pewnego pakietu udziałów w spółce z.o.o., posiadanego przez inwestora XYZ, pięć lat temu wynosiła 200000 zł. Po upływie tego okresu udziały zostały odsprzedane za 400000 zł. Jakie zatem musiałoby być oprocentowanie lokaty, na którą wpłacono 200000 zł, aby po 5 latach podwoić wartość wkładu? Odpowiedź to 14,87%, jest to CAGR. Przykłady obliczeń przedstawione zostaną w dalszej części artykułu.
Formalna definicja średniej rocznej stopy wzrostu powinna obejmować niezbędne elementy teorii wartości pieniądza w czasie. Moim zdaniem, powinno się zatem stwierdzić, że CAGR to stopa, przy której wartość pewnego kapitału początkowego zwiększyłaby się do znanej, przyszłej wartości tego kapitału, na przestrzeni danego okresu, przy rocznej kapitalizacji odsetek.
CAGR jest bardzo często wykorzystywana w ramach budżetowania kapitałowego. Oznacza to, iż miara ta znajduje zastosowanie w analizie opłacalności inwestycji. W niektórych przypadkach, może również posłużyć do wyznaczenia wysokości wymaganej stopy zwrotu. CAGR nie jest stosowany w księgowości, jest to miara, którą zainteresowani są analitycy i inwestorzy, ponieważ można ją wykorzystać w procesach decyzyjnych związanych z realizacją różnych przedsięwzięć inwestycyjnych.
CAGR – wzór
Wzór służący do obliczenia średniej rocznej stopy wzrostu przedstawiany jest na kilka sposobów. Niezależnie od sposobu prezentacji formuły, CAGR oblicza się w każdym przypadku w bardzo podobny sposób. Ewentualne różnice w kalkulacji wynikają z doboru danych, a nie z faktu, że w określonych przypadkach korzysta się z innego wzoru. Bardzo często, w źródłach inernetowych (np. Wikipedia) formuła przedstawiana jest w następujący sposób:

Powyższa formuła bardzo dokładnie określa parametry, które niezbędne są do przeprowadzenia obliczeń. Niemniej jednak, w mojej opinii nie jest ona wystarczająco intuicyjna, co jest spowodowane stosunkowo skomplikowanym zapisem. Oczywiście, powyższy wzór jest bardzo użyteczny, co przedstawię na przykładzie w dalszej części artykułu. Niemniej jednak, aby lepiej zrozumieć istotę CAGR, należy przeanalizować poniższe równanie: Powyższa formuła jest rezultatem przekształcenia wzoru na wartość przyszłą. Mianowicie, do ustalenia tej wielkości należy znać stopę procentową („i”), liczbę lat („t”), a także wielkość kapitału początkowego („PV”, np. wkład na lokatę). We wzorze na wartość przyszłą, CAGR odpowiada stopie procentowej. Dlatego też, aby ją obliczyć, należy przekształcić wzór dzieląc obie strony równania przez „PV”, a następnie podnosząc je do potęgi „1/t”, w następujący sposób:
Powyższa formuła jest rezultatem przekształcenia wzoru na wartość przyszłą. Mianowicie, do ustalenia tej wielkości należy znać stopę procentową („i”), liczbę lat („t”), a także wielkość kapitału początkowego („PV”, np. wkład na lokatę). We wzorze na wartość przyszłą, CAGR odpowiada stopie procentowej. Dlatego też, aby ją obliczyć, należy przekształcić wzór dzieląc obie strony równania przez „PV”, a następnie podnosząc je do potęgi „1/t”, w następujący sposób:
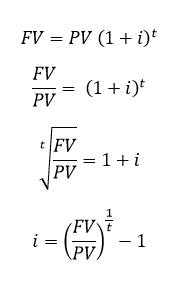
Powyżej „i”, czyli stopa procentowa jest średnią roczna stopą wzrostu. Zaznaczam, że CAGR nie koniecznie musi być stosowana tylko i wyłącznie w przypadku danych, które dotyczą lat. Korzystając z przedstawionego wzoru można również obliczyć okresową stopę. Na przykład, podstawiając liczbę kwartałów (zamiast lat) otrzymamy wartość skumulowanego kwartalnego wskaźnika wzrostu. Zastosowanie tego rozwiązania miałoby sens, gdyby dana inwestycja generowała kwartalne przepływy pieniężne. Podkreślam jednak, że z definicji, CAGR dotyczy okresów rocznych i jest stosowany jako, pewnego rodzaju, podsumowanie danej inwestycji. Dlatego też, aby nie wprowadzać zbędnego chaosu, w przykładach będę korzystał wyłącznie z danych rocznych.
CAGR – przykłady
Poniżej przedstawione zostaną przykłady obliczeń średniej rocznej stopy wzrostu. Będą one rozwinięciem przypadku, który został opisany we wstępie do artykułu. Rozważona zostanie zatem pewna inwestycja w udziały przedsiębiorstwa, których wartość w kolejnych pięciu latach oszacowano na podstawie wyceny rynkowej:
- Na początku inwestycji (t=0) wartość udziałów wynosi 200000 zł, ponieważ za taką kwotę zostały nabyte.
- Po roku (t=1) ich wartość wynosi 270000 zł.
- Po dwóch latach (t=2) ich wartość wynosi 250000 zł.
- Po trzech latach (t=3) ich wartość wynosi 340000 zł.
- Po czterech latach (t=4) ich wartość wynosi 350000 zł.
- Po pięciu latach (t=5) ich wartość wynosi 400000 zł.
Należy wyjaśnić, że CAGR można również obliczyć na przykładzie innych danych. Między innymi, mogą to być przychody przedsiębiorstwa, lub okresowe zyski z inwestycji. Niemniej jednak, najbardziej intuicyjne i miarodajne rezultaty dostarcza analizy pewnej wielkości, która zmienia się w czasie. Np. wartość akcji, udziałów, jednostek uczestnictwa w funduszach inwestycyjnych, surowców, itp.
Przykład 1
We wstępie przeanalizowany został przykład inwestora, który posiadał udziały w przedsiębiorstwie. Zgodnie z przedstawionymi danymi, ich wartość na początku inwestycji wynosiła 200000 zł, natomiast po pięciu latach aż 400000 zł. W tym przypadku wykorzystany zostanie drugi z przedstawionych wzorów. CAGR należy obliczyć w następujący sposób:
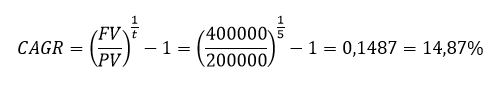
Oznacza to, że średnia roczna stopa wzrostu dla tej inwestycji wynosi 14,87%. Odzwierciedla ona wygładzony, roczny przyrost wartości udziałów na przestrzeni 5 lat, przy rocznej kapitalizacji odsetek. Można dodać, że przy stopie równej 14,87% w rozpatrywanym okresie można podwoić wartość inwestycji. Ten rezultat bardzo łatwo zweryfikować wykorzystując do tego wzór na wartość przyszłą:
Przykład 2
W drugim przykładzie zastosowany zostanie pierwszy z przedstawionych wzorów. Wymagać tego będzie treść zadania. Mianowicie, średnia roczna stopa wzrostu zostanie obliczona wyłącznie na podstawie wybranych danych. W poprzednim przykładzie, CAGR policzony został dla całego, pięcioletniego okresu. Natomiast, w tym przypadku, stopa oszacowana zostanie na podstawie dwuletniego okresu, rozpoczynającego się od „t=2” i kończącego w „t=4”. Oznacza to, że w początkowej fazie wartość udziałów wynosiła 250000 zł, a w końcowej 350000 zł. Obliczenia należy przeprowadzić w następujący sposób:
 Wartość kapitału początkowego przeciętnie przyrastała o 18,32% rocznie, przy uwzględnieniu rocznej kapitalizacji odsetek. Należy pamiętać, że jest to pewne uogólnienie, ponieważ CAGR odzwierciedla jedynie przeciętny, geometryczny przyrost. Rezultat można zweryfikować podstawiając wartość kapitału początkowego do wzoru na wartość przyszłą. Obliczenia można przeprowadzić w następujący sposób:
Wartość kapitału początkowego przeciętnie przyrastała o 18,32% rocznie, przy uwzględnieniu rocznej kapitalizacji odsetek. Należy pamiętać, że jest to pewne uogólnienie, ponieważ CAGR odzwierciedla jedynie przeciętny, geometryczny przyrost. Rezultat można zweryfikować podstawiając wartość kapitału początkowego do wzoru na wartość przyszłą. Obliczenia można przeprowadzić w następujący sposób:
Podsumowanie przykładów
Rezultaty obliczeń odzwierciedlają wygładzony, przeciętny zysk inwestora. W rzeczywistości, wartość udziałów, lub np. akcji, bardzo często zmienia się na przestrzeni wieloletniego okresu. Na poniższych rysunkach zestawiono rzeczywistą wartość analizowanych udziałów, a także wielkości, które obliczono ze wzoru na wartość przyszłą przy CAGR, dla każdego roku inwestycji. Interesujące jest, że CAGR nie uwzględnia wahań, które mają miejsce pomiędzy początkiem i końcem inwestycji. Mianowicie, metoda ta, bazuje tylko i wyłącznie na wartości początkowej i końcowej.


Jak obliczyć CAGR w arkuszu kalkulacyjnym?
Średnią roczną stopę wzrostu łatwo jest obliczyć w arkuszu kalkulacyjnym, tj. np. Microsoft Excel, lub inne podobne programy. Kalkulacje można przeprowadzić wprowadzając wzór bezpośrednio do arkusza, lub za pomocą kilku dostępnych funkcji. Poniżej, w kolejnych podpunktach przedstawione zostaną cztery, różne metody przeprowadzenia obliczeń. Wszystkie rozwiązania będą dotyczyć wcześniej zaprezentowanych przykładów, czyli fikcyjnej inwestycji w udziały przedsiębiorstwa, których wartość zmienia się na przestrzeni 5 lat.
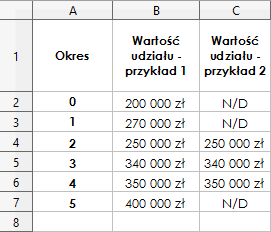
Pierwszym krokiem jest wprowadzenie danych do arkusza. Poniżej na rysunku przedstawiono tabelę, która zawiera niezbędne informacje. Istotne jest, że dane dotyczące omawianych przykładów przedstawiono osobno, w dwóch kolumnach. Należy przypomnieć, że w przykładzie pierwszym CAGR obliczany jest dla całego okresu. Natomiast w kolejnym, wyłącznie na podstawie danych pochodzących z okresu 2 i 4.
Metoda 1 – wprowadzenie wzoru do arkusza
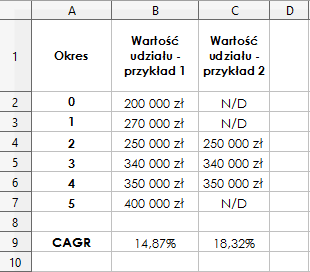
Pierwsza metoda obliczenia wartości CAGR polega na wprowadzeniu formuł do arkusza kalkulacyjnego, które odzwierciedlają wcześniej przedstawione wzory. W tym celu należy wykorzystać przedstawione dane, odwołując się do odpowiednich miejsc w tabeli. Obliczenia zostały przeprowadzone pod zestawieniem, w komórkach B9 i C9. Poniżej, na rysunkach, przedstawione zostały rezultaty, a także formuły, które wprowadzono do arkusza kalkulacyjnego.

Metoda 2 – zastosowanie funkcji IRR
CAGR można obliczyć stosując funkcje IRR, która wykorzystywana jest do oszacowania wartości wewnętrznej stopy zwrotu. Obliczenia przeprowadza się w bardzo nieskomplikowany sposób, niemniej jednak, wcześniej należy odpowiednio przygotować dane wejściowe. Mianowicie, należy usunąć wartości pochodzące z okresów, które nie dotyczą początku i końca inwestycji. W ich miejsce należy wstawić „0”. Dodatkowo, wartość z pierwszego okresu powinna być ujemna. Odpowiednio przygotowaną tabelę przedstawiono na poniższym rysunku. Grafika obejmuje również rezultaty, które powinny wyć wynikiem wprowadzenia prawidłowych formuł.
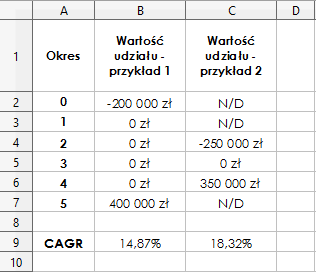
W komórki „B9” i „C9” wprowadzono funkcje IRR. Jej składania nie jest skomplikowana. Wymaga jedynie podania zakresu obserwacji, którymi są dane dotyczące wartości udziałów w spółce z.o.o. Dlatego też, w przykładzie pierwszym, jedynym argumentem będzie wektor „B2:B7”, natomiast w przykładzie drugim „C4:C6”. Na poniższym rysunku przedstawiono formuły, które należy wprowadzić do arkusza.

Metoda 3 – zastosowanie funkcji STOPA (RATE)
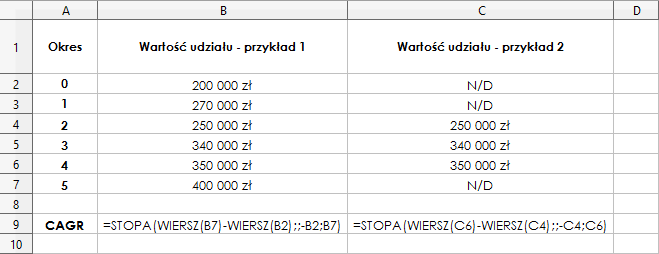
Skumulowany roczny wskaźnik wzrostu można również obliczyć za pomocą funkcji STOPA. Bardzo istotne jest, że nazwa tej metody różni się w poszczególnych arkuszach kalkulacyjnych. Na przykład, w arkuszu LibreOffice należy zastosować funkcje STOPA, natomiast w Microsoft Excel, zamiast STOPA, powinno się wykorzystać funkcje RATE. Ważne jest, że obydwie metody mają taką samą składnie i różnią się jedynie nazwą.
Do przeprowadzenia obliczeń należy wykorzystać podstawowy zestaw danych – taki sam, jak w przypadku metody nr 1. Oczywistym jest, że rezultaty będą identyczne. Należy pamiętać, o poprawnym wprowadzeniu wszystkich argumentów w składnie funkcji STOPA, lub inaczej RATE (liczba_okresów, rata, wb; [wp]; [typ], [wynik]):
- liczba_okresów – w przykładzie pierwszym jest ona równa 5, natomiast w drugim 2.
- rata – ten argument należy pominąć, ponieważ w przykładach nie występują żadne okresowe płatności.
- wb – wprowadzamy wartość początkową inwestycji ze znakiem minus, co oznacza, że w przykładzie nr 1 będzie to -200000, natomiast w drugim -250000.
- [wp] – jest to wartość końcowa inwestycji, w przykładzie nr 1 wynosi 400000, natomiast w drugim 350000.
- [typ], [wynik] – argumenty należy pominąć.
Istotne jest, że w obliczeniach można wykorzystać dodatkową funkcję – WIERSZ. Pozwala ona na zastosowanie relatywnych odwołań do wartości, które mają informować o liczbie okresów, w których realizowana jest inwestycja. Funkcja ta umożliwia uniknięcie ręcznego wprowadzenia liczby okresów w składnie funkcji. Poniżej, na rysunku, przedstawiono opisywane formuły.
Metoda 4 – zastosowanie funkcji POTĘGA
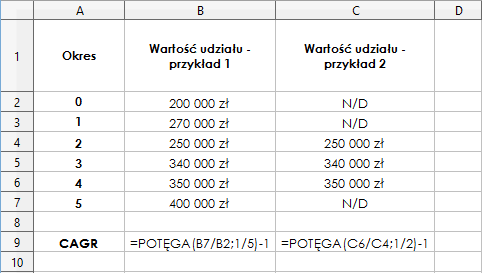
Innym rozwiązaniem jest zastosowanie funkcji POTĘGA. W dużym stopniu przypomina ono wprowadzenie wzoru do arkusza, które przedstawiono w ramach opisu metody nr.1. Jednak, w tym przypadku, funkcja POTĘGA pozwala zaoszczędzić trochę czasu, ponieważ jej składnia jest nieskomplikowana. Mianowicie, wymagane jest podanie wyłącznie dwóch argumentów: wartości, która ma zostać podniesiona do potęgi, a także potęgi. Przykład zastosowania tej funkcji został przedstawiony na poniższym rysunku. Należy zaznaczyć, że metoda wymaga wykorzystania podstawowego zakresu danych, którego nie trzeba w żaden sposób przekształcać. Istotne jest, że we wprowadzonej formule, od funkcji POTĘGA należy odjąć 1, co jest zgodne z przedstawionymi wzorami.
O czym należy pamiętać obliczając CAGR?
Średnia roczna stopa wzrostu jest relatywnie nieskomplikowaną miarą, która znajduje wiele zastosowań w praktyce. Należy jednak pamiętać, iż nie odzwierciedla ona rzeczywistej stopy zwrotu z danej inwestycji. CAGR jest jedynie pewnego rodzaju uogólnieniem, który ułatwia określenie, jak zyskowne jest dane przedsięwzięcie. Mianowicie, w rzeczywistości rynkowej, każda inwestycja charakteryzuje się stosunkowo dużymi fluktuacjami wartości. W jednym okresie można zaobserwować jej wysokie wzrosty, a już w kolejnym znaczne spadki. W takim przypadku CAGR, może pomóc opisać daną inwestycje i w przybliżeniu określić, jakie przeciętne stopy zwrotu ona generuje.
Skumulowany roczny wskaźnik wzrostu nie powinien być stosowany w oderwaniu od innych miar. Posiada on pewne wady, które mogą spowodować, że dana inwestycja zostanie nieprawidłowo scharakteryzowana. CAGR jest miarą, która nie uwzględnia zmienności danej inwestycji, tylko ukazuje wygładzony przeciętny przyrost jej wartości. Należy pamiętać, że wspomniana zmienność charakteryzuje ryzyko danego przedsięwzięcia, które jest jego niezmiernie ważną cechą. Każdy inwestor powinien zawsze wziąć te kwestie pod uwagę przy podejmowaniu decyzji dotyczącej realizacji danego przedsięwzięcia.
Dodatkowo należy pamiętać, że CAGR bazuje wyłącznie na wartościach historycznych. Rezultaty analizy nie dają żadnej gwarancji, że w przyszłości taka stopa zwrotu zostanie zrealizowana. Ponadto, na wyniki obliczeń, bardzo duży wpływ ma wybór początkowego okresu, który zostanie uwzględniony w obliczaniach. Jeżeli dana inwestycja we wcześniejszych okresach generowała straty, to brak ich uwzględnienia spowoduje, że CAGR będzie bardzo zawyżony. Dlatego też, dobór ram czasowych analizy powinien być bardzo przemyślany.
Plik arkusza kalkulacyjnego z danymi i rezultatami:
CAGR



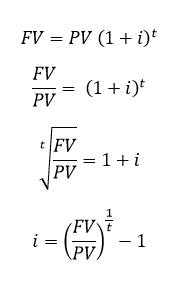
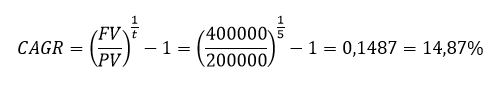













Mogę prosić o podanie bibliografii? 🙂
Witam.
Niestety w przypadku tego artykułu nie korzystałem z pozycji książkowych, ponieważ CAGR jest wypadkową wzoru na wartość przyszłą (procent składany). Te elementy teorii wartości pieniądza w czasie są opisywane w większości podręczników do matematyki finansowej. W artykule, jedynie w celach poglądowych, ukazałem wersję wzoru, którą można odnaleźć w Internecie (a dokładniej na Wikipedii). Niemniej jednak, pod tą formułą, przedstawiłem jej wyprowadzenie z teorii wartości pieniądza w czasie ).
Pozdrawiam,
Michał